Never forget about complexity analysis

In computer science, complexity analysis is the process of determining the computational complexity of algorithms, that is, the amount of resources (such as time and storage) required to execute them. Complexity analysis is a fundamental in the field of algorithm design and analysis. It allows us to understand the behavior of algorithms, and to predict the resources required to execute them.

There are two main types of complexity analysis: asymptotic analysis and exact analysis.

Asymptotic analysis

Asymptotic analysis is a way of understanding the behavior of an algorithm in the limit, as the input size goes to infinity. In other words, it allows us to understand how the algorithm scales with input size.

Asymptotic analysis is typically performed using big-O notation. This notation allows us to express the complexity of an algorithm as a function of the input size. For example, we might say that an algorithm is O(n2), which means that the algorithm’s complexity is proportional to the square of the input size.

Exact Analysis

Exact analysis is a way of determining the exact resources required to execute an algorithm for a given input size.Exact analysis is typically performed using exact arithmetic. This allows us to compute the exact resources required to execute an algorithm for a given input size.

In small word

Both asymptotic and exact analysis are important tools in the design and analysis of algorithms. Asymptotic analysis is typically used to understand the behavior of an algorithm in the large, while exact analysis is used to understand the behavior of an algorithm in the small. Asymptotic analysis is typically easier to perform, and it provides a more general understanding of an algorithm’s behavior. However, it can be difficult to use asymptotic analysis to predict the behavior of an algorithm for small input sizes. Exact analysis is more difficult to perform, but it can be used to predict the behavior of an algorithm for any input size. In general, complexity analysis is an important tool in the design and analysis of algorithms. It allows us to understand the behavior of algorithms, and to predict the resources required to execute them.

Big-O Analysis of Algorithms

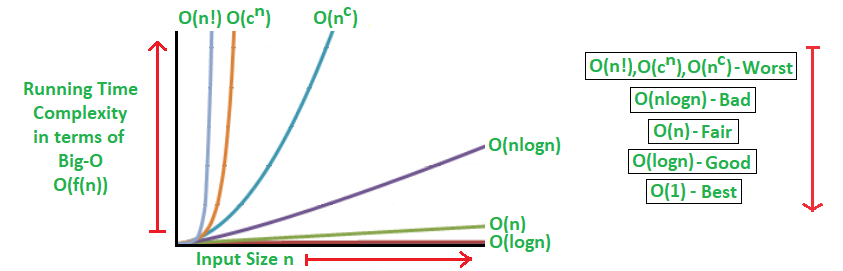
There are different ways to measure the performance of an algorithm. In general cases, we mainly used to measure and compare the worst-case theoretical running time complexities of algorithms for the performance analysis. The fastest possible running time for any algorithm is O(1), commonly referred to as Constant Running Time. In this case, the algorithm always takes the same amount of time to execute, regardless of the input size. This is the ideal runtime for an algorithm, but it’s rarely achievable. In actual cases, the performance (Runtime) of an algorithm depends on n, that is the size of the input or the number of operations is required for each input item. The algorithms can be classified as follows from the best-to-worst performance (Running Time Complexity):

A logarithmic algorithm – O(logn)
Runtime grows logarithmically in proportion to n.

A linear algorithm – O(n)
Runtime grows directly in proportion to n.

A superlinear algorithm – O(nlogn)
Runtime grows in proportion to n.

A polynomial algorithm – O(nc)
Runtime grows quicker than previous all based on n.

A exponential algorithm – O(cn)
Runtime grows even faster than polynomial algorithm based on n.

A factorial algorithm – O(n!)
Runtime grows the fastest and becomes quickly unusable for even
small values of n.